 |
The Music of Life
Mike Keith |
Introduction
The Game of Life is a well-known "zero-person game" invented by John H. Conway. It is "played" on an infinite square grid, each cell of which can be in one of two states - alive or dead. Initially, some finite number of cells are marked as alive, and then succeeding "generations" of the life colony are generated according to the following two rules:
1. A live cell stays alive if it currently has either 2 or 3 live neighbors (the "neighbors" of a cell are the eight surrounding cells); otherwise, it dies.
2. A cell that is currently dead becomes alive on the next generation if it currently has exactly 3 neighbors.
The fascinating thing about Life is its unpredictability. Some initial configurations die out quickly, some enter periodic repeating states, and others churn around for a long time before eventually settling down. And this unpredictability is not just empirical: it has been proven that determining the fate of an initial Life population is equivalent to Turing's Halting Problem, which is formally undecidable. In others words, it really is impossible to determine Life's fate!
(For more on Life see volume 2 of the book Winning Ways by Berlekamp, Conway, Guy, or some of the Life pages on the Web such as these.)
Life into Music
An interesting feature, from a musical point of view, is the tension between the two life rules: Rule One makes the population go down by killing cells, whereas Rule Two makes the population go up via births. If we plot the total population of a Life colony over the successive generations, we get a curve that tends to go up and down somewhat erratically before (usually) settling down to a constant or a repeated pattern. Such a somewhat-erratic-but-also-somewhat-well-behaved curve is reminiscent of the shape of musical melodies.
Here is an example. Suppose we start with the following configuration of live cells:
oooooooooooooo oooooooooooooooooo o o o o o o oooo oo ooo ooo oo oo ooooooooooooo o o ooo ooo ooo oo o o o o o o oo ooooo ooo ooo oooo o o o o o o ooo o ooo ooo oo o o oooooooooooooo oooo ooo ooo ooooo o o o o o o ooo oooo ooo ooo o o o o o o o o o o o oo ooo ooo o oo ooooooooooooooooooooooooooooooooo
This pattern is a very famous one known as a "Garden of Eden", because it can be shown (not easily) that there does not exist a Life pattern that yields this pattern on the next generation. This pattern has 226 live cells; if we let it run for the next 135 generations we find that the population counts are as follows:
226 90 159 111 197 116 175 139 218 148 205 160 200 150 169 160 152 136 141 131 138 138 129 112 111 121 117 141 119 131 120 121 122 135 137 132 127 126 116 122 119 120 121 119 113 108 107 94 88 87 88 108 99 112 113 119 120 119 108 122 112 110 113 91 96 97 89 85 96 84 96 84 75 72 77 81 98 100 103 98 105 107 101 114 118 123 130 135 129 145 118 117 127 143 127 146 153 131 147 126 119 133 132 121 138 123 147 134 134 141 150 119 123 117 120 104 99 107 93 92 89 89 65 61 57 63 69 67 65 55 51 47 43 41 37
with the pattern now entering a stable state, so the population remains 37 forever after. More musically suggestive is a graph of these numbers, which looks not unlike the contour of a melody:
Garden of Eden
Population Graph
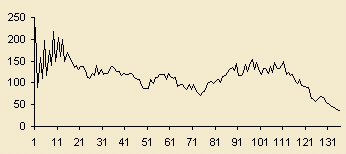
When we have long sequences of integers there are several ways to reduce them to become short musical melodies, which usually involve some kind of digital filter. In this case we just use simple subsampling (which corresponds to a degenerately simple digital filter). We take every 5th number from the table above starting with the second one (the 90). Finally, we must reduce the magnitude of the numbers; this is done with simple linear scaling, via the function
f(n) = [(n-37)/20]
where [ ] is the greatest-integer function. The resulting numbers are interpreted as notes in the 7-tone major scale, with 0=root, 1=next note, etc. Of course we chose the "-37" in the formula so the the last note of the tune would be a 0, thus ending on the traditional root of the major scale.
Here are the notes of our tune, written in the key of G and 3/4 time:
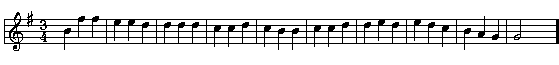
If you are equipped to play General MIDI (.mid) files, here is a simple arrangement for flute and piano. In this version, the pitches are exactly as shown in the music above, but the durations have been altered a little to make it less monotonous. In other words, most of what you hear is still determined by the mathematical process; I've just spiced it up a bit.